2021.06.17 네이버 블로그에 게시했던 글을 이전한 게시글입니다.
일 관련으로 가까운 점을 검색하는 법을 찾고 있던 와중에
얼핏 보기에 비슷해 보이는 알고리즘 세 개가 있어 공부 겸 비교해보았다.
데이크스트라 알고리즘(Dijkstra algorithm)
최단경로 알고리즘 또는 다익스트라 알고리즘이라고도 불린다.
지도 등에서 최단 경로를 찾을 때 사용된다.
출발점에서 도착점까지 최단경로로 가야할때,
갈 수 있는 루트가 A,B,C가 있다고 한다.

① 우선 갈 수 있는 모든 루트를 무한으로 잡는다.

② 이웃하고있는 모든 루트를 방문하여 거리를 계산한다.

출발점에서 인접하고있는 모든 루트는 A와 B가 된다.

따라서 현재의 최단거리를 가진 점은 A이며 비용은 각각 11, 12가 된다

③ 가장 거리가 적은 루트를 저장해둔 다음 계속 이웃한 점의 거리를 구한다.
현재는 A가 가장 가깝기에 A를 최단점으로 지정한다.

최단점이 지정되었다면, 다시 루프를 돌아 인접 점들의 거리를 확인한다.

B에서 C를 경우하는 경우가 A를 통하는 경유보다 거리가 짧기때문에
최단 거리는 B,C를 거치는 루트가 된다.
이 작업을 반복하여 최단 거리를 구한다.
플러드 필 알고리즘(FloodFill)
다차원 배열의 특정 칸과 연결된 영역을 찾는 알고리즘.

그림판/포토샵의 "페인트 도구"에 자주 사용된다.
① 보라색 테두리 안의 영역을 녹색으로 채우고싶다고 한다.

② 우선 특정 영역을 기준으로 잡는다.
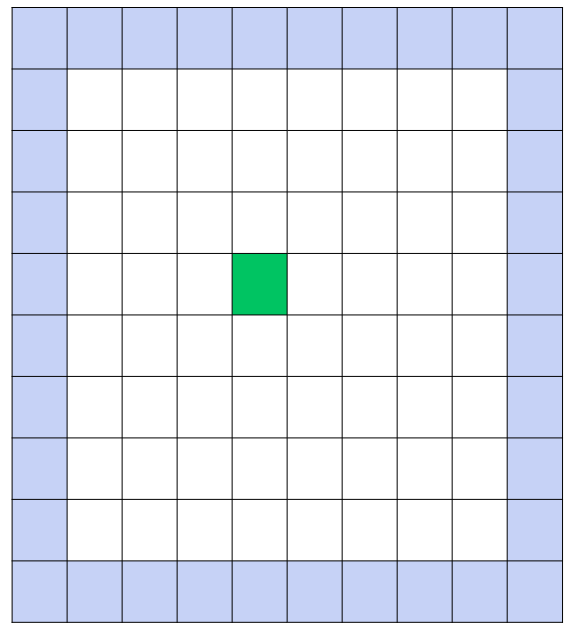
③ 영역의 상,하,좌,우를 큐에 넣는다.

④ 다음 큐의 위치로 이동한다

⑤ 역시 상하좌우를 큐에 넣는다.
그러나 하는 이미 색이 칠해져 있으므로 큐에 넣지않아도 된다.
⑥ 이를 반복하여 색을 채워나간다

최근접쌍 문제(Closet Pair Problem)
아래와 같이 무작위로 점이 존재할 때, 가장 가까운 점 두개를 고를 때 사용된다.
일반적으로 점 하나하나를 비교하면 시간이 오래걸리므로, 비교하는 점의 갯수를 줄여 시간을 줄이는 방식이다.
아래의 점의 집합이 있다고 한다.

① 점의 갯수를 반으로 나눌 수 있는 점 하나를 정한다.
위치가 중앙이 아니어도 되기에 점 P[n/2]로 정한다.

② 나눠진 그룹 내에서 점들끼리 거리를 비교하여 가장 거리가 짧은 점들을 구한다

중앙점을 기점으로 나눈 점들끼리 길이를 비교한다.
③ 그룹내에서 가장 거리가 짧은 점 한쌍을 각각 지정한다.
예시에선 임의로 두 쌍을 정해 각각 거리가 2, 3이라고한다.

④ 마지막으로 양쪽그룹에 있는 점들중에 거리값이 더 작은 쌍이 있는지 찾는다.

세 알고리즘의 비교
데이크스트라, 플러드필, 최근접점쌍 알고리즘을 비교하면 아래와 같다
● 데이크스트라
- 출발점과 도착점이 정해져있을 경우 유용하다.
- 도착점까지 이동 중, 여러 점을 지나가는 '경유'를 생각해야 할 경우 사용된다.
●플러드 필
- 특정 영역을 채워야할 때 사용하면 유용하다.
- 게임의 경우 파이프에 물이 지나가는 길이나 미로 전체에 가스가 퍼진다거나할때 물 또는 가스가 이동하는 루트 설정에 사용될 수 있다.
●최근접점쌍
- 많은 점들 중 가장 거리가 가까운 한쌍을 찾는데 유용하다.
- 하지만 3D좌표상에는 z축의 거리도 생각해야하므로 번거로운 과정을 거쳐야할 수 있다.